Cardinal sequences of LCS spaces under GCH

Juan Carlos Martinez, Lajos Soukup

Let ${\mathcal C}(\alpha)$ denote the class of all cardinal sequences of length $\alpha$ associated with compact scattered spaces. Also put

$${\mathcal C}_{\lambda}(\alpha)=\{f\in {\mathcal C}(\alpha): f(0)={\lambda} = \min[ f({\beta}) : \beta < {\alpha}]\}.$$

If ${\lambda}$ is a cardinal and ${\alpha}<{\lambda}^{++}$ is an ordinal, we define ${\mathcal D}_{\lambda}(\alpha)$ as follows: if ${\lambda}={\omega}$ ,

$${\mathcal D}_{\omega}(\alpha)=\{f\in {}^{\alpha}\{{\omega},{\omega}_1\}: f(0)={\omega}\},$$

and if ${\lambda}$ is uncountable,

$$\begin{multline}\notag {\mathcal D}_{\lambda}({\alpha})=\{f\in {}^{\alpha}\{{\la... ...t{ is $<{\lambda}$-closed and successor-closed in ${\alpha}$} \}. \end{multline}$$

We show that for each uncountable regular cardinal ${\lambda}$ and ordinal ${\alpha}<{\lambda}^{++}$ it is consistent with GCH that ${\mathcal C}_{\lambda}(\alpha)$ is as large as possible, i.e.

$${\mathcal C}_{\lambda}(\alpha)={\mathcal D}_{\lambda}(\alpha).$$

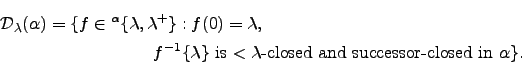
This yields that under GCH for any sequence $f$ of regular cardinals of length ${\alpha}$ the following statements are equivalent:

(1)

$f\in {\mathcal C}(\alpha)$ in some cardinal preserving and GCH-preserving generic-extension of the ground model.

(2)

for some natural number $n$ there are infinite regular cardinals $\lambda_0>\lambda_1>\dots>\lambda_{n-1}$ and ordinals ${\alpha}_0,\dots, {\alpha}_{n-1}$ such that ${\alpha}={\alpha}_0+\cdots+{\alpha}_{n-1}$ and $f=f_0\mathop{{}^{\frown}\makebox[-3pt]{}}\ f_1\mathop{{}^{\frown}\makebox[-3pt]{}}\cdots \ \mathop{{}^{\frown}\makebox[-3pt]{}}f_{n-1}$ where each $f_i\in{\mathcal D}_{\lambda_i}(\alpha_i)$ .

The proofs are based on constructions of universal locally compact scattered spaces.

Key words and phrases:locally compact scattered space, superatomic Boolean algebra, cardinal sequence, universal

2000 Mathematics Subject Classification: 54A25, 06E05, 54G12, 03E35, 03E05

Downloading the paper